An object that consists of both magnitude and direction can be termed as a vector. For example, in a line segment that is directed, length defines the magnitude of the vector whereas the pointed arrow indicates its direction. Any two vectors are said to be the same when their magnitudes and directions are the same. Velocity and force can be the perfect illustrations of the concept of a vector. Different operations can be performed on vectors namely addition, subtraction and multiplication.
The addition of two vectors involves adding any two given vectors say a and b. The commutative and associative properties are satisfied by the addition of vectors. Vector subtraction is defined as the method of obtaining the difference of vectors and is also the inverse of the addition of vectors. A scalar say k is multiplied by vector a to arrive at ka. Scalar multiplication fulfils the same properties as that of normal multiplication.
- k (a + b) = ka + kb (by distributive law)
- (s + t) k = sk + tk (by distributive law)
- 1 * a = a
- (−1) * a = − a
- 0 * a = 0
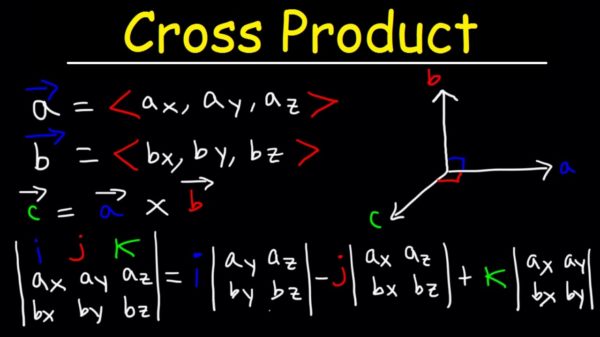
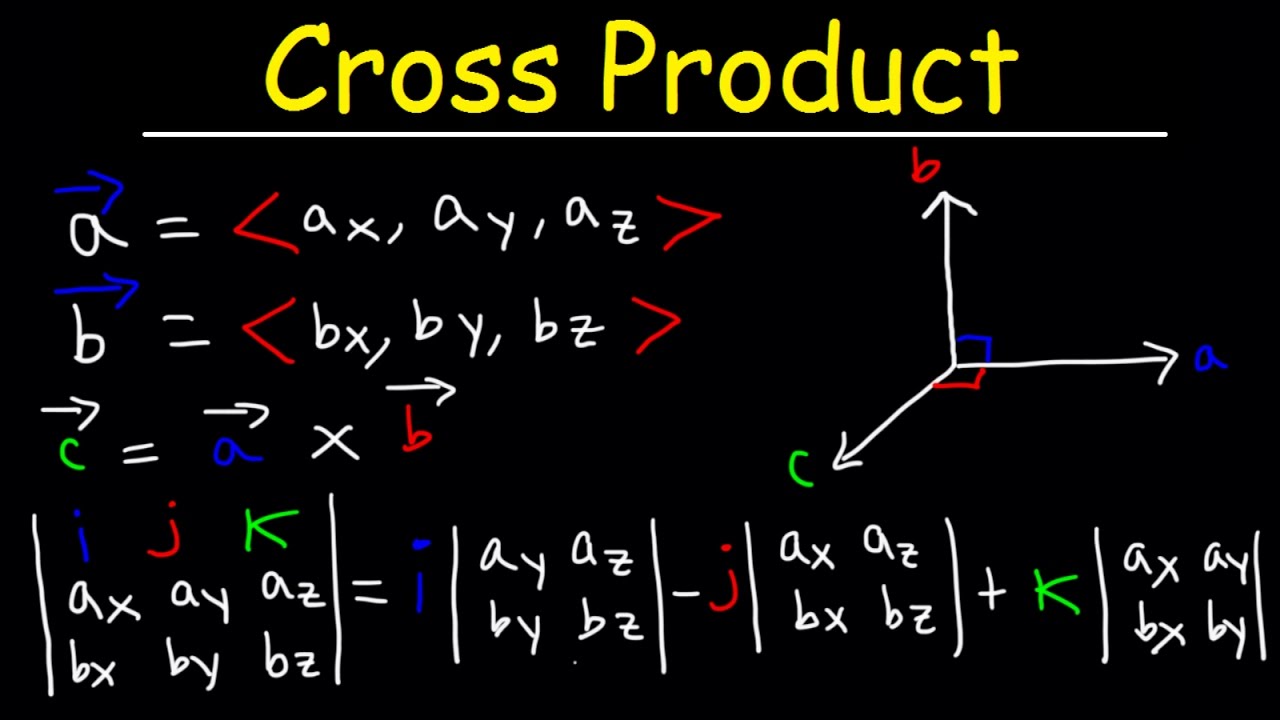
There exist two processes of getting the product of two given vectors. The methods are a method of the cross product and dot product. The concept of the cross product is applicable for 3d vectors only. The cross product is denoted a × b (a cross b). The cross product thus obtained is also a 3d vector. It is guided by the following requirements.
- a × b (a cross b) is perpendicular to both vectors a and b.
- The direction of a × b (a cross b) is explained by the right-hand rule.
- The area of the parallelogram spanned by the two given vectors a and b defines the magnitude of the vectors.
The area of the parallelogram spanned by the two given vectors a and b is given by ||a|| ||b|| sin θ, where the angle between the vectors is θ.
Assume the two vectors as a and b.
a = a1i + a2j + a3k
b = b1i + b2j + b3k
Their cross product of a cross b = (a1i + a2j + a3k) × (b1i + b2j + b3k)
= a1b1 (i × i) + a1b2 (i × j) + a1b3 (i × k) + a2b1 (j × i) + a2b2 (j × j) + a2b3 (j × k) + a3b1 (k × i) + a3b2 (k × j) + a3b3 (k × k)
Properties of cross product are as follows:
- The cross product of a vector with itself results in a zero vector.
- It is non-commutative.
- Cross product is distributive over addition.
- It is not associative.
- Cross product satisfies the Jacobi property.
Vector dot product
The projection of one vector on the other provides a foundation for the dot product. The amount of projection of vector a towards a unit vector u defines the dot product of vector a with the unit vector u. The vector dot product is also termed as a scalar product. Consider two non-zero vectors A and B. The vector product is given by AB cos θ.
Properties of vector dot product are given below.
- It is commutative.
- The vector dot product is distributive over addition.
- It is not associative.
Few applications of vector dot product include the calculation of mechanical work = vector dot product of force and displacement vectors, also power = vector dot product of force and velocity vectors. Please visit BYJU’S for more information on vectors and their uses.